Question

A heptagon has unequal sides that are in a pattern. Each side is 2 more than twice the side of the smaller one before it. Write the expression of the perimeter.

Answer 1

Heptagon has unequal sides and each side is 2 more than twice the side of the smaller one before it.

Heptagon is a 2 dimensional geometric shape that has got 7 sides.

Lets say the length of smallest side is 'x' units.

Length of the second side will be 2 more than twice the smaller side so the side length will be:

`2* x+2=2x+2`

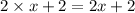
Now the length of the third side will be 2 more than twice the second side that is:

`2(2 * x+2)+2=2(2x+2)+2=4x+4+2=4x+6`

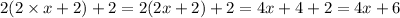
Similarly, length of the fourth side will be:

`2(4x+6)+2=8x+12+2=8x+14`

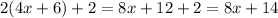
Similarly, length of the fifth side will be:

`2(8x+14)+2=16x+28+2=16x+30`

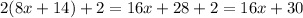
Again, length of the sixth side will be

`2(16x+30)+2=32x+60+2=32x+62`

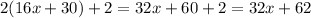
And the length of the seventh side will be

`2(32x+62)+2=64x+124+2=64x+126`

Now, perimeter of any geometric shape is the sum of the lengths of the sides:

Adding all the sides we get:

`x+(2x+2)+(4x+6)+(8x+14)+(16x+30)+(32x+62)+(64x+126)`

`=x+2x+2+4x+6+8x+14+16x+30+32x+62+64x+126`

`=127x+240`

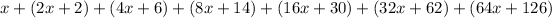
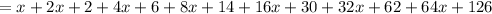
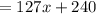
Therefore, the expression for the perimeter of the required heptagon is
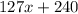`127x+240`.