Answer:
3.9 m³
Explanation:
To find the volume of a right prism, multiply its base area by its height.
For the given shape:
- Base = trapezoid ABCD
- Height = 1.5 m
Area of a trapezoid
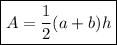
Where a and b are the bases and h is the height.
From inspection of the given diagram:
- a = BC = 1.7 m
- b = AD = 2.3 m
- h = CD = 1.3 m
Substitute the given values into the formula to find the area of the trapezoid base (ABCD):
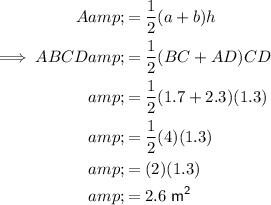
Therefore:
