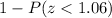Which is equivalent to
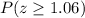
Solution: The equivalent expression for
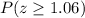 is
is
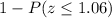
Step-by-step explanation:
The complement rule of probability states that the sum of the probabilities of an event and it's complement mus equal to 1.
Let
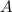 be an event and
be an event and
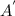 be its complement. Then using the complementary rule, we have:
be its complement. Then using the complementary rule, we have:
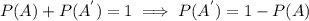
Using the same complementary rule in the given example:
We have:
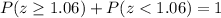
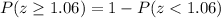
Therefore, the equivalent expression for
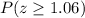 is
is