Question

A SAMPLE DATA SET HAS A MEAN OF 122.3 AND A STANDARD DEVIATION OF 18.5. CONVERT A SCORE OF 168.4 TO A Z SCORE AND DETERMINE IF THE SCORE IS "USUAL" OR "UNUSUAL"

1.23; USUAL
-1.23; USUAL
D.49; UNUSUAL
-2.49; UNUSUAL

Answer 1

Z- score of the sample is 2.49, Unusual.

Solution-

We know the formula for calculating Z score,

`Z=(X- \mu)/(\sigma)`

where,

X = raw score = 168.4

μ = mean of the sample = 122.3

σ = standard deviation of the sample = 18.5,

Putting all the values in the equation,

`Z = (168.4-122.3)/(18.5) = 2.49`

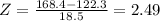
∵ According to the rule, if the Z-score is lower than -1.96 or higher than 1.96 (or its absolute value greater than 1.96 ) then it is considered as unusual and interesting.

Here, as the value of Z is more than 1.96 which is 2.49, so it's unusual.

Answer 2

Given mean =122.3 and standard deviation =18.5

`z=(x-mean)/(standard deviation) = (168.4-122.3)/(18.5)`

`= (46.1)/(18.5)`

≈2.49

As a general rule z-scores lower than -1.96 or higher than 1.96 are considered unusual.

Since our z-score = 2.49>1.96 , it is unusual.

Hence correct option is 'C' = "2.49 ; unusual"