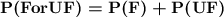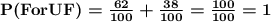Question

In a local survey, 100 citizens indicated their opinions on a revision to a local land-use plan. Of the 62 persons giving favorable responses, 40 were males. Of the 38 giving unfavorable responses, 15 were males. If one citizen is randomly selected, find the probability that person has a favorable opinion or has an unfavorable opinion

Answer 1

Answer: The probability that a randomly selected citizen has a favorable or unfavorable opinion is 1 or 100%.

In this question, we have only two answers favorable or unfavorable.

A person can't have both opinions at the same time.

So these events - favorable and unfavorable are mutually exclusive events i.e one event cannot occur when the other occurs.

Let P(F) be the probability of a person who has a favorable opinion

P(UF) be the probability of a person who has an unfavorable opinion

`\boldsymbol{\mathbf{P(F) = (Total people with favorable responses)/(Total people in the survey)}}`

`\boldsymbol{\mathbf{P(F) = (62)/(100)}}`

`\boldsymbol{\mathbf{P(UF) = (No. of people with unfavorable opinion)/(Total number of people in the survey)}}`

`\boldsymbol{\mathbf{P(UF) = (38)/(100)}}`

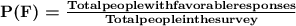
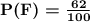
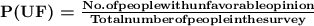
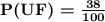
Now, the probability of either one of two mutually exclusive events occurring is:

`\boldsymbol{\mathbf{P(F or UF) = P(F) + P(UF)}}`

`\boldsymbol{\mathbf{P(F or UF) = (62)/(100) + (38)/(100) = (100)/(100)=1}}`