Question

"a man drove 10 mi directly east from his home, made a left turn at an intersection, and then traveled 2 mi north to his place of work. if a road was made directly from his home to his place of work, what would its distance be to the nearest tenth of a mile?"

Answer 1

When you think of the situation as a whole, you may notice that the lines in the problem actually form a triangle. First, the man driving 10 miles east forms a bottom leg of the triangle 10 units long. When he drives the 2 miles north, he adds another leg of 2 units length. When the place of work is connected to the starting position through a line, a third and final line is drawn which creates the triangle.

So, how can we find the direct distance from his place of work to his home? We can use the Pythagorean Theorem (
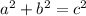`a^2 + b^2 = c^2`, where
`a` and
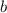`b` are the lengths of the legs of the triangle and
`c` is the length of the hypotenuse). We know that the lengths of the legs are 10 and 2, which we can use in the formula, as shown below:

`(10)^2 + (2)^2 = c^2`

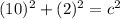
Now, we can solve this equation for
`c`:

`√((10)^2 + (2)^2) = c`

`√(104) = c \approx 10.2`

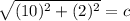
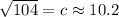
The distance would be √104 miles, or approximately 10.2 miles.