Answer: -17.7 m/s
The maximum height achieved by balloon,
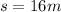
The instantaneous velocity at the maximum height,
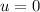
The balloon free falls under gravity,
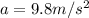
Using the equation of motion:
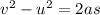
where,
 is the final velocity,
is the final velocity,
 is the initial velocity,
is the initial velocity,
 is the acceleration and
is the acceleration and
 is the distance covered.
is the distance covered.
Substitute the values:
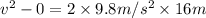
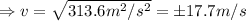
We will consider only the negative value, as the positive direction is considered upwards.