Question

Solve the system by elimination

Answer 1

First of all we will eliminate x from our equations. In order to do that we will use our first and second equation and then we will use second and third equation.

`-2x+2y+3z=0...(1)\\-2x-y+z=-3....(2)`

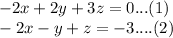
Upon subtracting 2 equation from 1 we will get,

`3y+2z=3....(4)`

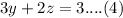
Now we will use second and third equation to eliminate x.

`-2x-y+z=-3....(2)\\2x+3y+3z=5....(3)`

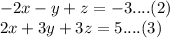
Adding 2nd and 3rd equation we will get,

`2y+4z=2....(5)`

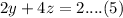
Now we will find out y from our 4th and 5th equation.

`2*(3y+2z)=2*3....(4)\\2y+4z=2....(5)`

Upon subtracting 5th equation from 4th equation we will get,

`4y=4\\y=1`

Now let us find out z by substituting y's value in 5th equation.

`2*1+4z=2\\4z=2-2\\z=0`

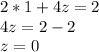
Now we will find x from by substituting y and z's value in equation 1.

`-2x+2*1+3*0=0\\-2x+2=0\\2=2x\\x=1`

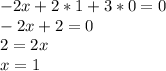
Therefore, x=1, y=1 and z=0 is the solution of the given system.