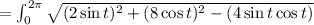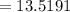Question

Find, correct to four decimal places, the length of the curve of intersection of the cylinder 4x2 1 y2 − 4 and the plane x 1 y 1 z − 2.

Answer 1

Answer- Length of the curve of intersection is 13.5191 sq.units

Solution-

As the equation of the cylinder is in rectangular for, so we have to convert it into parametric form with

x = cos t, y = 2 sin t (∵ 4x² + y² = 4 ⇒ 4cos²t + 4sin²t = 4, then it will satisfy the equation)

Then, substituting these values in the plane equation to get the z parameter,

cos t + 2sin t + z = 2

⇒ z = 2 - cos t - 2sin t

∴
`(dx)/(dt) = -\sin t`

`(dy)/(dt) = 2 \cos t`

`(dz)/(dt) = \sin t-2cos t`

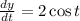
As it is a full revolution around the original cylinder is from 0 to 2π, so we have to integrate from 0 to 2π

∴ Arc length

`= \int_(0)^(2\pi)\sqrt{((dx)/(dt))^(2)+((dy)/(dt))^(2)+((dz)/(dt))^(2)`

`=\int_(0)^(2\pi)\sqrt{(-\sin t)^(2)+(2\cos t)^(2)+(\sin t-2\cos t)^(2)`

`=\int_(0)^(2\pi)\sqrt{(2\sin t)^(2)+(8\cos t)^(2)-(4\sin t\cos t)`

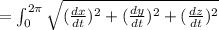
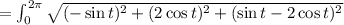
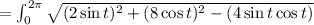
Now evaluating the integral using calculator,

`=\int_(0)^(2\pi)\sqrt{(2\sin t)^(2)+(8\cos t)^(2)-(4\sin t\cos t)`
`= 13.5191`