This is a difference of squares. Every time you have the difference between two squares, you can factor it as the product between the sum and the difference of the roots:
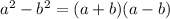
In your case, the squares are
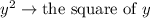
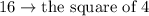
So, the difference between the squares,
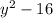 can be written as the multiplication between the sum and difference of the roots:
can be written as the multiplication between the sum and difference of the roots:
