Question

I have 12 more nickels than quarters. If the coins are worth $5.40, how many nickels are there?

Answer 1

Let's try to create two equations to help us solve this problem. For this problem,
`n` will represent the number of nickels and
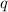`q` will represent the number of quarters.

A first one could represent the number of coins we have. This does not regard the value of the coins, but rather just how many we could count. Based on the information in the problem, we could say:

`n = 12 + q`

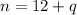
After all, the number of nickels is 12 more than the number of quarters.

Now, let's create an equation to represent the value of the coins we have. Since each
`n` nickel is worth 5 cents, we can say the value of all the nickels in cents is
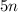`5n`. We can thus say for quarters that the value of all quarters in cents is
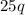`25q`. Since we know the value of the coins we have adds to $5.40, or 540 cents, we can say:

`5n + 25q = 540`

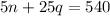
Now, we have two equations:

`n = 12 + q`

`5n + 25q = 540`

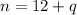
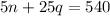
We can use substitution to find our answers:

`5(12 + q) + 25q = 540`

`60 + 5q + 25q = 540`

`30q + 60 = 540`

`30q = 480`

`q = 16`

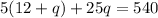
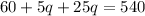
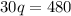
We have now found that the number of quarters we have is 16. When we use this value in one of our equations, we can find
`n`:

`n = 12 + q`

`n = 12 + 16 = 28`

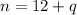
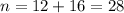
We have 16 quarters and 28 nickels.