Question

A car accelerates from 14 m/s to 21m/s in 6.0 s. What was its acceleration? How far did it travel in this time? Assume constant acceleration.

Answer 1

The acceleration of the car is
`1.17 m/s^2`

The car traveled 104.70 m in 6 seconds with constant acceleration.

Step-by-step explanation:

Initial speed of the car = u = 14 m/s

Final speed of the car = v = 21 m/s

Acceleration of the car in in 6 seconds = a

t = time = 6 seconds

Using first equation of motion:

`v=u+at`

`21 m/s=14 m/s+a*6s`

`7 m/s=a* 6s`

`a=(7 m/s)/(6 s)=1.1667 m/s^2\approx 1.17m/s^2`

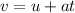
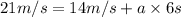
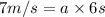
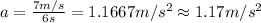
The acceleration of the car is
`1.17 m/s^2`

Distance traveled by the car in 6 seconds: = s

Using third equation of motion:

`v^2-u^2=2as`

`(21 m/s)^2-(14 m/s)^2=2* 1.2 m/s^2* s`

`s=((21 m/s)^2-(14 m/s)^2)/(2* 1.17 m/s^2)=104.70 m`

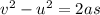
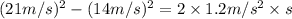
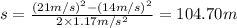
The car traveled 104.70 m in 6 seconds with constant acceleration.

Answer 2

Step-by-step explanation:

It is given that,

Initial velocity of the car, u = 14 m/s

Final velocity of the car, v = 21 m/s

Time taken, t = 6 s

Acceleration of the car is equal to the change in speed divided by time i.e. it can be written as :

`a=(v-u)/(t)`

`a=(21\ m/s-14\ m/s)/(6\ s)`

a = 1.166 m/s²

or

a = 1.17 m/s²

For finding how fat it travel in this time is calculated using third equation of motion :

`v^2-u^2=2as`

s = distance

`s=(v^2-u^2)/(2a)`

`s=(21^2-14^2)/(2* 1.17)`

s = 104.7 m

Hence, the acceleration of the car is 1.166 m/s² and distance covered by it is 104.7 m