From t= 0 to t=2, distance is a straight line, and hence speed is slope of that line.
Hence for 0<=t<2, speed =
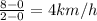
From 2<=t<=2.5, distance remained constant at 8km, hence speed is 0 km/h.
From 2.5<=t<3, distance again a straight lines.
And hence speed = slope of line joining (2.5,8) and (3,10)
=

From 3<=t<4, distance remained constant at 10km. That means he is at rest.
Hence speed = 0 km/h for 3<=t<=4.
From 4<=t<5, distance again is a straight line.
Hence speed = slope of line joining (4,10) and (5,12)
=
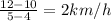
Please refer the graph for speed.