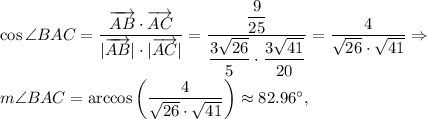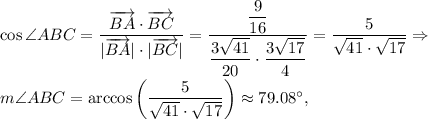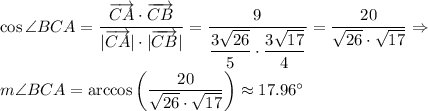You are given the plane
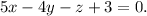
1. To find x-intercept, you have to substitute y=z=0 into the plane's equation:
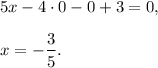
2. To find y-intercept, you have to substitute x=z=0 into the plane's equation:
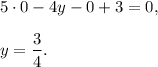
3. To find z-intercept, you have to substitute y=z=0 into the plane's equation:
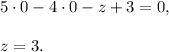
You get three points of intersection with coordinate axises:
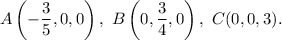
The lengths of sides are:
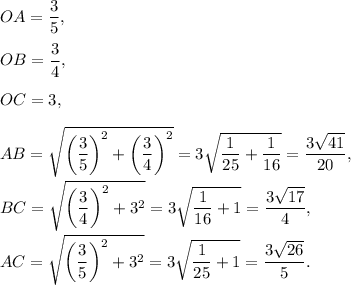
To find angles consider vectors:
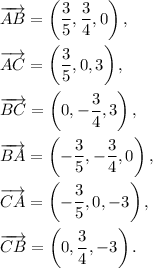
Then