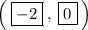Question

Solve by substituton

Answer 1

Solve the first equation for
`x`.

`x+3y = -2 \implies x = -3y - 2`

Substitute this into the second equation and solve for
`y`.

`-3(-3y-2) + y = 6 \implies 9y + 6 + y = 6 \implies 10y = 0 \implies y=0`

Now solve for the value of
`x`.

`x = -3\cdot0 - 2 = -2`

So the solution to the system is the point
`(x,y) = \boxed{(-2,0)}`

Answer 2

`\left( \: \boxed{-2}\:, \: \boxed{0} \: \right)`

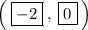
Explanation:

Given system of equations:

`\begin{cases}x+3y=-2\\-3x+y=6 \end{cases}`

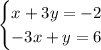
To solve using the method of substitution, solve one equation for one of the variables.

Solving equation 2 for y:

`\implies -3x+y=6`

`\implies -3x+y+3x=3x+6`

`\implies y=3x+6`

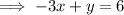
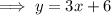
Substitute this expression into the other equation and solve for x:

`\implies x+3y=-2`

`\implies x+3(3x+6)=-2`

`\implies x+9x+18=-2`

`\implies 10x+18=-2`

`\implies 10x+18-18=-2-18`

`\implies 10x=-20`

`\implies 10x / 10=-20 / 10`

`\implies x=-2`

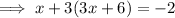
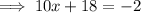
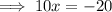
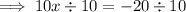
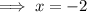
Substitute the found value of x into the expression for y, and solve for y:

`\implies y=3x+6`

`\implies y=3(-2)+6`

`\implies y=-6+6`

`\implies y=0`

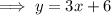
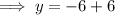
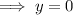
Therefore, the solution to the given system of equations is:

`\left( \: \boxed{-2}\:, \: \boxed{0} \: \right)`