Answer: The equation in point slope form is y-6 = x-3
Step-by-step explanation: The general equation of a line in point slope form is y - y1 =m(x -x1)
where m is the slope and (x1,y1) is the point
Given point (3,6) and (-2,1)
We know slope of a line when two points are given
m=
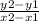
where (x1,y1) and (x2,y2) are the two points
Here m=
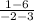
=
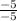
m=1
Now the equation of line
y-6 = 1 (x-3)
i.e. y-6 = x-3