Question

The point (2,8) is on the graph of f(x)=x3. What is the value of b if the point (0.5,8) is on the graph of f(bx)?

If the point (1,3) is on the graph of y=f(x), then what is the corresponding point on the graph of y=−2f(x)?

Answer 1

1) Given
`f(x) = x^(3)`

`f(bx) = (bx)^(3)= b^(3)  x^(3)`

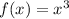
Since (0.5,8) lies on f(bx) ,
`8=b^(3) 0.5^(3)`

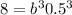
Divide with
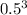`0.5^(3)` on both sides

`b^(3) = (8)/(0.5^(3) )`

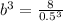
= 64

`b=64^{(1)/(3) } = 4`

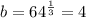
Hence b=4.

2) Given (1,3) lies on y=f(x) plugin x=1 and y=3

that is f(1) = 3

We can find corresponding point for that in y=-2f(x) by plugging in x=1.

That is y= -2f(1) = -2*3 = -6

Hence point is (1,-6)