The roots of the equation are:
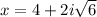 and
and

Step-by-step explanation
Roots means the solutions or the values of x.
Given equation:
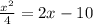
First multiplying both side by 4, we will get...
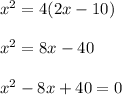
As the above equation is a quadratic equation in form of
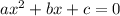 , so
, so
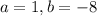 and
and
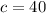
Using quadratic formula...
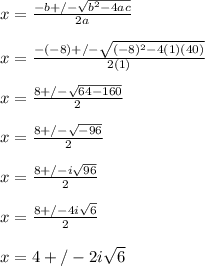
So, the roots of the equation are:
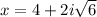 and
and
