Question

Special precision bolts are made by another machine. These are for jobs that require more exact measurements. The bolts must be within 0.01 mm of 8 mm. This is represented by |x – 8| < 0.01. 


Write this inequality as a compound inequality without absolute value bars.






Solve the inequality.






Graph the solutions on a number line.






What do the solutions of the inequality mean for the bolt?

Answer 1

The absolute value of a number
`x` is the positive version of that number. So, if
`x` is positive, its absolute value is
`x` itself. If
`x` is negative, its absolute value is
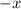`-x`, so that it will be positive again.

So, if the absolute value of a number is smaller than a certain quantity, i.e.
`|x|<a` it means that the positive version of
`x` is less than
`a`.

So, if
`x` is positive, the inequality becomes
`x<a`. If
`x` is negative, the inequality becomes
`-x<a \iff x>-a`.

So, as a compound inequality, we have

`|x|<a \iff -a<x<a`

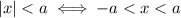
So, in your case, we have

`|x-8|<0.01 \iff -0.01 < x-8 < 0.01`

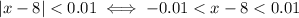
Add 8 to all sides in this inequality:

`8-0.01 < x < 8+0.01 \iff 7.79 < x <8.01`

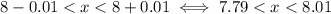
So, on a number line, you must higlight all numbers between 7.79 and 8.01, endpoints excluded.

Conceptually, this means that the bolt measurement should be exactly 8mm, but you can accept bolts that are 0.01 millimeters shorter of larger.