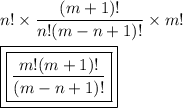Question

Suppose
`m` men and
`n` women are to be seated in a row so that no two women sit together. If
`m\ \textgreater \ n`, show that the number of ways in which they can be seated is:
`(m!(m+1)!)/((m-n+1)!)`

Answer 1

Firstly, we'll fix the postions where the
`n` women will be. We have
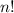`n!` forms to do that. So, we'll obtain a row like:

`\underbrace{\underline{~~~}}_(x_2)W_2 \underbrace{\underline{~~~}}_(x_3)W_3 \underbrace{\underline{~~~}}_(x_4)... \underbrace{\underline{~~~}}_(x_n)W_n \underbrace{\underline{~~~}}_{x_(n+1)}`

The n+1 spaces represented by the underline positions will receive the men of the row. Then,

`x_1+x_2+x_3+...+x_(n-1)+x_n+x_(n+1)=m~~~(i)`

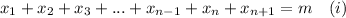
Since there is no women sitting together, we must write that
`x_2,x_3,...,x_(n-1),x_n\ge1`. It guarantees that there is at least one man between two consecutive women. We'll do some substitutions:

`\begin{cases}x_2=x_2'+1\\x_3=x_3'+1\\...\\x_(n-1)=x_(n-1)'+1\\x_n=x_n'+1\end{cases}`

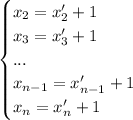
The equation (i) can be rewritten as:

`x_1+x_2+x_3+...+x_(n-1)+x_n+x_(n+1)=m\\\\ x_1+(x_2'+1)+(x_3'+1)+...+(x_(n-1)'+1)+x_n+x_(n+1)=m\\\\ x_1+x_2'+x_3'+...+x_(n-1)'+x_n+x_(n+1)=m-(n-1)\\\\ x_1+x_2'+x_3'+...+x_(n-1)'+x_n+x_(n+1)=m-n+1~~~(ii)`

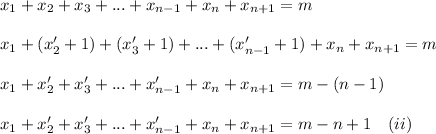
We obtained a linear problem of non-negative integer solutions in (ii). The number of solutions to this type of problem are known:
`([(n)+(m-n+1)]!)/((n)!(m-n+1)!)=((m+1)!)/(n!(m-n+1)!)`

[I can write the proof if you want]

Now, we just have to calculate the number of forms to permute the men that are dispposed in the row:
`m!`

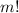
Multiplying all results:

`n!*((m+1)!)/(n!(m-n+1)!)* m!\\\\ \boxed{\boxed{(m!(m+1)!)/((m-n+1)!)}}`