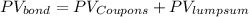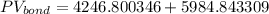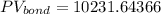Question

A 10-year us treasury bond with a face value of $10,000 pays a coupon of 5.5% (2.75% of face value every 6 months). the semiannually compound interest rate is 5.2% (a six-month discount rate of 5.2/2 = 2.6%). what is the present value of the bond?

Answer 1

Answer: The Present Value of the bond is $10,231.64.

We have

Face Value of the bond $10000

Coupon rate per year 5.5%

Frequency of int payments Semi-Annual (two periods in a year)

Discount rate per year 5.2%

No. of years to maturity 10 years

First we calculate the coupon interest per period

`C = Face Value * (interest rate)/(2)`

`C = 10000 * (0.055)/(2)`

`C = 10000 * (0.055)/(2)`

`C = 10000 * 0.0275`

`C = 275`

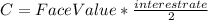
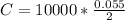
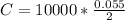
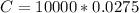
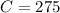
We can think of a bond as an instrument have types of cash flows.

One is the coupons we receive from a bond, where we receive a fixed amount per period for a stated number of periods.

An instrument that gives a fixed amount per period for a stated number of periods is known as an annuity.

Hence we can treat the coupon from the bonds as an annuity.

The Present Value formula for an annuity is:

`PV_(Coupons) = C\left \{ (1-(1+i)^(-n))/(i) \right\}`

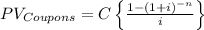
where

C = Coupon per period

i = discount rate per period

n = number of periods

In this question, we'll get
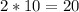`2*10 =20` coupon payments, so the number of periods, n = 20.

The discount rate per period (i) is
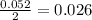`(0.052)/(2) = 0.026` or 2.6% per period.

Applying these values to the equation above we can find the PV of Coupons as:

`PV_(Coupons) = 275\left \{ (1-(1+0.026)^(-20))/(0.026) \right\}`

`PV_(Coupons) = 275\left \{ (1-(1+0.026)^(-20))/(0.026) \right\}`

`PV_(Coupons) = 275\left \{ (0.598484331)/(0.026) \right\}`

`PV_(Coupons) = 275 * 15.44291035`

`PV_(Coupons) = 4246.800346`

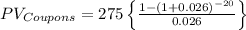
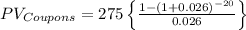
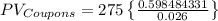
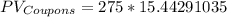
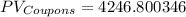
In addition to the coupon, we also get back the bond's face value at the end of the bond's life. We can treat this as a lump-sum amount we will get back at the end of a stated number of periods. We can find the Present Value of the lumpsum as follows:

`PV = (Face Value)/((1+i)^(n))`

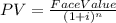
Substituting the values we get,

`PV = (10000)/((1+0.026)^(20))`

`PV = (10000)/(1.670887521)`

`PV_(lump sum) = 5984.843309`

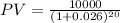
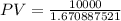
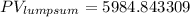
Finally, we compute the Present Value of the bond as follows:

`PV_(bond) = PV_(Coupons) + PV_(lump sum)`

`PV_(bond) = 4246.800346 + 5984.843309`

`PV_(bond) = 10231.64366`