To find the area of a rectangle, we multiply the Base by the Height. In this case the: Base = AB and Height = BC
So to get the area, we multiply AB by BC. (and we know that BC = 5x+5/x+3 and BC = [3x+9/2x-4)
So we would do:
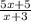 x
x

Note: When multiplying fractions together, we multiply the numerator by the numerator, and the denominator by the denominator.
For example
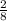 x
x
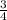 =
=
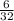
Answer:
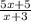 x
x
 =
=
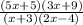
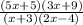 =
=
 [Note: we are able to factorise some brackets to make the sum easier. For example we can factor out the 5 in (5x+5) to get: 5(x+1) ]
[Note: we are able to factorise some brackets to make the sum easier. For example we can factor out the 5 in (5x+5) to get: 5(x+1) ]
Now lets simplify by multiplying the 5 and 3 together in the numerator:
 =
=
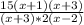
If you notice, there is a (x+3) in numerator and the denominator. This means that we can cancel out the (x+3), to get the most simplified expression for the area:
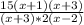 =
=

Final Simplified Answer:
 which is the last option
which is the last option