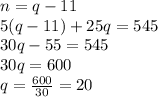If Kendra were to add 11 more nickels, she would have equal numbers of quarters and nickels, so a multiple of $0.30. Adding $0.55 to her total would give her $5.45 + 0.55 = $6.00, which is 20 times $0.30. At that point she would have 20 quarters and 20 nickels. But we know 20 nickels is 11 more than the number she really has, so ...
Kendra has 9 nickels and 20 quarters.
_____
If you want to write equations, you can let n and q stand for the numbers of nickels and quarters Kendra has.
... 5n +25q = 545 . . . . . the amount of money Kendra has
... q = n+11 . . . . . . . . . . . the relationship between numbers of quarters and nickels
Using the second equation to substitute for q in the first, we have
... 5n +25(n+11) = 545
... 30n +275 = 545
... 30n = 270
... n = 270/30 = 9
... q = n + 11 = 9 + 11 = 20
If you were to work this problem substituting for n instead of q, you would find the equations match the logic used in the text description above.