Question

A current of 0.86 a flows through a copper wire 0.47 mm in diameter when it is connected to a potential difference of 15 v. how long is the wire?

Answer 1

To calculate the length of the wire, we use formulas,

`R = (V)/(I)` (A)

`R= \rho  (l)/(A)` (B)

Here, R is the resistance of the wire, I is the current flows through wire and V is potential difference. A is cross sectional area of wire and
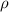`\rho` is the density of copper wire and is value,
`\rho = 1.7* 10^(-8) \Omega m`.

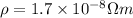Given
`I = 0.86 A,V=15 V and  r = (0.47 mm)/(2) =2.35 * 10^(-4) m, V= 15 V.`

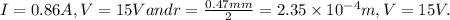
Substituting the values of I and V in equation (A ) we get,

`R=(15V)/(0.86A) = 17.44 \Omega`

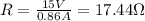
Now from equation (B),

`l=(R A)/(\rho )`

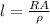
Therefore,

`l= (17.44*\pi * r^2  )/(1.7* 10^(8) \Omega m) \\\\ l= (17.44* 3.14 *(2.35*10^(-4)m)^2  )/(1.7* 10^(-8) \Omega m) = 177.9 m`

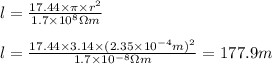
Thus the length of the copper wire is 177.9 m.