Question

According to the Rational Root Theorem, what are all the potential rational roots of f(x) = 5x3 – 7x + 11?

Answer 1

The answer is B " +/- 1/5 , +/- 1 , +/- 11/5 , +/- 11 "

Answer 2

We will determine the roots of the given equation
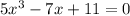`5x^3-7x+11=0` by rational root theorem.

Rational root theorem states:

"If P(x) is a polynomial with integer coefficients, then p is a factor of the constant term of P(x) and q is a factor of the leading coefficient of P(x).Then all the possible values of
`(p)/(q)` are the factors of the given polynomial".

Therefore, the given equation is:

`5x^3-7x+11=0`

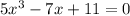
The factors of the leading coefficient of
`x^3` = q =
`\pm 1, \pm 5`

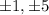
The factors of the constant = p =
`\pm 1, \pm 11`

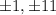
So, the possible values of
`(p)/(q) = \pm 1 , (\pm 1)/(\pm 5),{\pm 11}, (\pm 11)/(\pm 5)`.

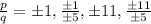Therefore, the roots of the given polynomial are
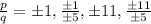`(p)/(q) = \pm 1 , (\pm 1)/(\pm 5),{\pm 11}, (\pm 11)/(\pm 5)`.