Register
If m<PQT=60 and m<PQS=4x+14 find the value if x
34.6k views
5 votes
If m<PQT=60 and m<PQS=4x+14 find the value if x

User Gabr
by
5.2k points

1 Answer

7 votes

Diagram is attached below

m<PQT=60 and m<PQS=4x+14

m<PQS and m<SQT are same

m<PQT = m<PQS + m<SQT = m<PQS + m<PQS = 2m<PQS

m<PQT = 2m<PQS

So m<PQS =
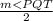
(m<PQT)/(2)

Plug in the given information and solve for x

4x + 14 =
(60)/(2)

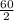
4x + 14 = 30 (subtract 14 on both sides)

4x = 16 (Divide by 4 on both sides)

x = 4

The value of x is 4

If m<PQT=60 and m<PQS=4x+14 find the value if x-example-1
User Igor Berman
by
6.2k points
Ask a Question
Welcome to QAmmunity.org, where you can ask questions and receive answers from other members of our community.

5.9m questions

7.7m answers

Other Questions

Solve for y in terms of x. 2/3y - 4 = x y = x + 6 y = -x + 4 y = -x + 6 y = x + 4
Aliyah has $24 to spend on seven pencils. After buying them she had $10. How much did each pencil cost?
Use the normal model ​n(11371137​,9696​) for the weights of steers. ​a) what weight represents the 3737thth ​percentile? ​b) what weight represents the 9999thth ​percentile? ​c) what's the iqr of the weights
Evaluate a + b when a = –16.2 and b = –11.4 A. –27.6 B. –4.8 C. 4.8 D. 27.6
What is the value of x? (-4) - x = 5
Link Copied!