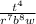Question

Simplify using only POSITIVE exponents:

1. (2x^3y^7)^-2

2. 12x^5y^3
--------------
4x^-1

3. (r^-7 B^-8)
---------------
(t^-4 w)

Answer 1

So here are a few rules with exponents that you should know:

1. Multiplying exponents of the same base:
   `x^m*x^n=x^(m+n)`
2. Dividing exponents of the same base:
   `x^m/ x^n=x^(m-n)`
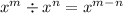
3. Powering a power to a power:
   `(x^m)^n=x^(m*n)`
4. Converting a negative exponent to a positive one:
   `x^(-m)=(1)/(x^m)\ \textsf{and}\ (1)/(x^(-m))=x^m`

1.

Firstly, solve the outside exponent:

`(2x^3y^7)^(-2)=2^(-2)x^(3*-2)y^(7*-2)=2^(-2)x^(-6)y^(-14)`

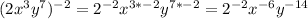
Next, convert the negative exponents into positive ones:

`2^(-2)x^(-6)y^(-14)=(1)/(2^2x^6y^(14))=(1)/(4x^6y^(14))`

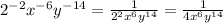
Your final answer is
`(1)/(4x^6y^(14))`

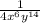
2.

For this, just divide:

`(12x^5y^3)/(4x^(-1))=(12)/(4)x^(5-(-1))y^(3-0)=3x^6y^3`

Your final answer is
`3x^6y^3`

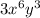
3.

For this, convert all negative exponents into positive ones:

`(r^(-7)b^(-8))/(t^(-4)w)=(t^4)/(r^7b^8w)`

Your final answer is
`(t^4)/(r^7b^8w)`