Question

The graph of the function h(x)= |x + 2| - 4 is shifted 3 units down. Draw the transformed function on the provided graph.

Answer 1

Always if you want to draw functions like this you should find the point that equals zero abs here that point is -2 so we have two line one of them is x-2 and the other is-x-6

Answer 2

Refer the attached figure.

The new function is
`h(x)= |x + 2| - 7`

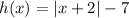
Explanation:

Given : The graph of the function
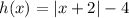`h(x)= |x + 2| - 4` is shifted 3 units down.

To find : Draw the transformed function on the provided graph?

Solution :

When the graph is shifted with 'b' unit downward then the function get subtracted by that unit,

`f(x)\rightarrow f(x)-b`

Applying in the given function,

`h(x)= |x + 2| - 4`

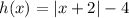
h(x) shifted 3 units down,

`h(x)= |x + 2| - 4-3`

`h(x)= |x + 2| - 7`

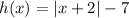
Refer the attached figure below for the graph and transformation of function.