Wow this one definitely tested me and was kind of tedious but I think I figured it out for you!
First times each term by the LCD which would be T(m)(n).
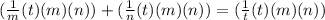
This cancels out the denominators and gives you a new equation.

This is where it got a little confusing but I moved the terms with m to one side so that they could be factored out to isolate m.
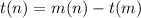
Factoring out the m from the two terms gives you this equation.
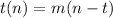
There is now only one term still connected to the m variable which can just be divided out. Giving you your final answer.
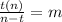
Hope this helped and was clear enough!
:)