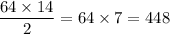Question

How many ways can i put down two indistinguishable pieces on an ordinary $8\times 8$ chessboard, if the pieces must either be in the same row or be in the same column?

Answer 1

The first piece can go in any of the 64 squares. The second piece can then be in any of 14 positions, since there are 7 unoccupied squares in the row of the first piece, as well as 7 unoccupied squares in the column of the first piece. This would seem to give us 64 · 14 choices for the placement of the two pieces. However, order doesn't matter (we said the pieces are indistinguishable), so the actual number of choices is (64 · 14)/2, which is 448.

Answer 2

Each of the 64 squares of the chessboard has 7 other squares in its same row, and 7 other squares in its same column.

So, for each of the 64 rows in which we can place the first piece, we have 14 choices for the square for the second piece.

But the pieces are indistinguishable, so we have to divide that number by two, because each combination has a "twin" one, where you flip the two pieces, obtaining the exact same combination.

So, the answer is

`(64* 14)/(2) = 64 * 7 = 448`