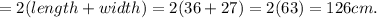Question

The ratio of the corresponding sides of two similar triangles is 4:9. the length of the smaller rectangle is 16 cm and its width is 12 cm. what is the perimeter of the larger rectangle

Answer 1

The perimeter of the larger rectangle is 126 cm.

Step-by-step explanation

The ratio of the corresponding sides of two similar rectangles is
`4:9`

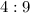
Given that, the length of the smaller rectangle is 16 cm and its width is 12 cm

Lets assume, the length and width of larger rectangle are
`x` and
`y` respectively.

(Length of smaller / Length of larger) = 4 : 9

`(16)/(x)=(4)/(9)\\ \\ 4x = 16*9\\ \\ 4x= 144 \\ \\ x= (144)/(4)=36`

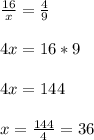
So, the length of larger rectangle is 36 cm.

(Width of smaller / Width of larger) = 4 : 9

`(12)/(y)=(4)/(9)\\ \\ 4y= 12*9\\ \\ 4y= 108\\ \\ y= (108)/(4)=27`

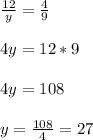
So, the width of larger rectangle is 27 cm.

Thus, the perimeter of the larger rectangle
`=2(length+width)= 2(36+27)= 2(63)=126 cm.`