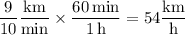Przykład 5.
a) The plot cross the horizontal line
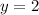 when the time is
when the time is
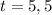 , so it took 5,5 s to cover the first 2 m.
, so it took 5,5 s to cover the first 2 m.
b) If
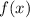 denotes the distance from the starting position of the object, then its average speed over the entire 6-s period is
denotes the distance from the starting position of the object, then its average speed over the entire 6-s period is
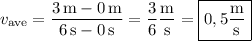
c) In the last 3 seconds, the object covers a distance of
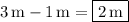
d) False. The average speed over the first 3-s period is
![v_(\rm ave[0,3]) = (1\,\mathrm m - 0\,\mathrm m)/(3\,\mathrm s - 0\,\mathrm s) = \frac13 (\rm m)/(\rm s) \approx 0,33 (\rm m)/(\rm s)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/sazs2jtttapvuozl97ph.png)
while over the second 3-s period, it is
![v_(\rm ave[3,6]) = (3\,\mathrm m - 1\,\mathrm m)/(6\,\mathrm s - 3\,\mathrm s) = \frac23 (\rm m)/(\rm s) \approx 0,66(\rm m)/(\rm s) \\eq 0,33(\rm m)/(\rm s)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ki877hxaioek32d5vewx.png)
Przykład 2.
In total there are
8 + 24 + 28 + 16 + 4 = 80
graded assignments. Compute the percentages of students whose scores fall into the given categories:
• 0-8 : 8/80 = 1/10 = 10/100 = 10%
• 9-16 : 24/80 = 3/10 = 30/100 = 30%
• 17-24 : 28/80 = 7/20 = 35/100 = 35%
• 25-32 : 16/80 = 1/5 = 20/100 = 20%
• 33-40 : 4/80 = 1/20 = 5/100 = 5%
See the attached pie chart.
Zadanie 3.
From the plot, it appears that Mateusz
• took 6 min to reach the bus stop
• waited for 2 min
• took 5 min to return home
• took 1 min to grab his notebook
• took 5 min to return to the bus stop
• waited for 3 min
• and after the bus arrives, moves further away over the next 4 min
This means the total time Mateusz needed to (1) return home to get the notebook, (2) find the notebook, and (3) return to the bus stop is
5 min + 1 min + 5 min = 11 min
Zadanie 4.
True. Mateusz walks the distance between his house and the bus stop within the first 6 min, which is 2/5 of 1 km = 0,4 km = 400 m.
True. The bus arrives after 22 min, and its average speed is equal to Mateusz's average speed over the next 4 min. At 22 min, he is 0,4 km from home, and at 26 min, he is 4 km away from home, so the average speed is
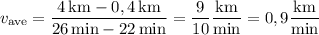
Convert the speed to km/h.