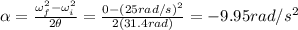Question

A wheel accelerates uniformly from rest to an angular speed of 25 rad/s in 10 s.(a) Find the angular acceleration of the wheel. (b) Find the tangential and radial acceleration of a point 10cm from the wheel’s center. (c) How many revolutions has the wheel turned during this time interval? (d) Then, find the wheel’s angular deceleration if it comes to a full stop after 5 rev

Answer 1

(a) Angular acceleration

The initial angular speed of the wheel is
`\omega_i=0`, the final angular speed is
`\omega_f=25 rad/s`, and the time taken is t=10 s. Therefore, the angular acceleration of the wheel is given by:

`\alpha=(\omega_f-\omega_i)/(t)=(25 rad/s-0)/(10 s)=2.5 rad/s^2`

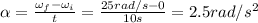
(b1) Tangential acceleration

The tangential acceleration is given by the product between the angular acceleration
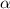`\alpha` and the distance from the wheel's center r. In this case,
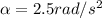`\alpha=2.5 rad/s^2` and
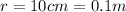`r=10 cm=0.1 m`, therefore the tangential acceleration is

`a_t=\alpha r=(2.5 rad/s^2)(0.1 m)=0.25 m/s^2`

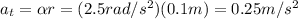
b2) Radial acceleration

The radial acceleration (also called centripetal acceleration) is given by:

`a_c =\omega^2 r`

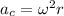
where
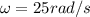`\omega=25 rad/s` is the final angular speed while r=0.1 m is the distance from the center of the wheel. Substituting numbers, we get

`a_c=\omega^2 r=(25 rad/s)^2(0.1 m)=62.5 m/s^2`

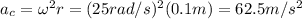
c) Number of revolutions

First of all, we need to find the angle covered during this time interval, which is given by:

`\theta=\omega_i t+ (1)/(2)\alpha t^2=(1)/(2) \alpha t^2=(1)/(2)(2.5 rad/s^2)(10 s)^2=125 rad`

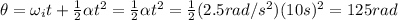
And keeping in mind that
`1 rev=2 \pi rad`, the number of revolutions made is:

`\theta = (125 rad)/(2 \pi rad/rev)=19.9 rev`

d) Deceleration

In this last part of the problem, we are told that the wheel comes to a stop after
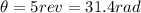`\theta=5 rev=31.4 rad`. We also know the initial angular speed,
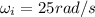`\omega_i =25 rad/s`, and the final angular speed,
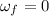`\omega_f=0`, so we can find the new angular (de)celeration by using the equation:

`2\alpha \theta=\omega_f^2-\omega_i^2`

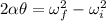
Substituting numbers, we get

`\alpha=(\omega_f^2-\omega_i^2)/(2\theta)=(0-(25 rad/s)^2)/(2(31.4 rad))=-9.95 rad/s^2`