Question

Find the equation for the plane through the points upper p 0 left parenthesis 1 comma negative 4 comma negative 3 right parenthesisp0(1,−4,−3)​, upper q 0 left parenthesis 5 comma negative 4 comma negative 2 right parenthesisq0(5,−4,−2)​, and upper r 0 left parenthesis negative 3 comma 1 comma 2 right parenthesisr0(−3,1,2).

Answer 1

3 points: (1, -4, -3), (5, -4, -2), (-3, 1, 2)

Explanation:

Answer 2

Given

3 points: (1, -4, -3), (5, -4, -2), (-3, 1, 2)

Find

The equation of the plane through these points.

Solution

Approach

There are (at least) a couple of ways you can go at this. One is to write the equation of the plane, substitute the given points, and solve for the values of the coefficients. This gives 3 linear equations in 4 unknowns, so one of the coefficients ends up being free choice. It will have only one possible value that makes the coefficients mutually prime integers.

Another approach is to find the cross product of two vectors that are in the plane. It is generally convenient to use the differences between pairs of points for this. The cross product will be the normal vector for the plane, so the remaining task is to make it go through one of the points and to adjust coefficients to be mutually prime.

In both cases, it is convenient to make use of a calculator that does matrix and/or vector math.

Equation Coefficients

We can write the equation of the plane as

... ax +by +cz = d

where a, b, c, d are mutually prime integers and a is positive. Without loss of generality, we can initially assume d=1. Substituting the given point values, we get three equations in a, b, c.

`a-4b-3c=1\\5a-4b-2c=1\\-3a+b+2c=1`

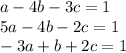
Using your favorite solution technique, you find*

... a=-5/31, b=-24/31, c=20/31

We can put the equation into standard form by multiplying it by -31 to get

... 5x +24y -20z = -31

Vectors

If we call the points in order A, B, C, then vector AB = (5-1, -4-(-4), -2-(-3)) = (4, 0, 1) and vector AC = (-3-1, 1-(-4), 2-(-3)) = (-4, 5, 5). The cross product of these is

... AB×AC = (-5, -24, 20) . . . . . matching our previous result

This is the normal vector for the plane of interest. It can be used directly for the coefficients of x, y, z, but we want the coefficient of x to be positive. So, we will use the opposite of this vector. Then the equation of the plane can be written using point A as a reference:

... 5(x -1) +24(y +4) -20(z+3) = 0

... 5x +24y -20z = -31

___

* Many calculators will give the result in decimal form, so finding the corresponding fraction can be tricky.