Question

Guys i need help making this quadratic equation into a standard form HELP ME PLEASE, ^2 means Like 2 Square.

1.) 11x^2 - 98 = 11 + 9x

2.) (2x - 1)^2 = (x + 4) ^2

3.) 4x^2 + 2x - 9 = (x - 2)(x - 9)

4.) 0 = 6 (x + 7)^2 - 58

5.) - 1/2 ( x - 1/4 )^2 + 12 = 0


​

Answer 1

1) 1x² - 9x - 109 = 0

2) 3x² -12x -15 = 0

3) 3x² + 13x - 27 = 0

4) 6x² + 84x + 236 = 0

5) -16x² + 8x + 383 = 0

Explanation:

The standard form of the quadratic equation is ax² + bx + c where a, b and c are constants.

So we have to convert each of the equations into a form that resembles the above

(1) 11x² -98 = 11 + 9x

• Simplify both sides of the equation.
  11x²−98 = 9x+11
  

• Subtract 9x+11 from both sides.
  11x²−98−(9x+11)=9x+11−(9x+11)
  ==> 11x² -98 -9x - 11 = 0
  ==> 11x² - 9x - 109 = 0 (Answer)
  with a = 11, b = -9, c = -109

(2) (2x - 1)² = (x + 4) ²

• Simplify both sides of the equation
  
  Using the fact that (a + b)²:
  (2x - 1 )² = 4x² -4x + 1 (a = 2x, b = -1)
  (x +4 )² = x² + 8x + 16 (a = x, b = 4)
  
  ==> 4x² -4x + 1 = x² + 8x + 16
  ==> 4x² -4x + 1 - (x² + 8x + 16) = 0
  ==> 4x² -4x + 1 - x² - 8x - 16 = 0
  ==> 3x² -12x -15 = 0 (Answer)
  With a=3, b=-12, c=-15
  

(3) 4x² + 2x − 9 = (x − 2)(x − 9)

• Simplify (x−2)(x−9)
  (x - 2) (X - 9) = x² - 9x - 2x + 18 (use FOIL method)
  
• 4x² + 2x − 9 = x² - 9x - 2x + 18 = x² - 11x + 18
  4x² + 2x - 9 - (x² - 11x + 18) = 0
  4x² + 2x - 9 - x² + 11x - 18 = 0
  3x² + 13x - 27 = 0 (Answer)

(4) 0 = 6(x +7 )² - 58

• Switch sides:
  6(x +7 )² - 58 = 0
  
• Simplify (x + 7)²
  (x + 7)² = x² + 14x + 49
  
  
• Simplify 6(x² + 14x + 49) - 58 = 0
  6(x² + 14x + 49) - 58 = 0
  ==> 6x² + 84x + 294 - 58 = 0
  ==> 6x² + 84x + 236 = 0 (Answer)
  with a = 6, b = 84 and c = 236
  

(5) -1/2 ( x - 1/4 )² + 12 = 0

• Calculate
  `-(1)/(2) (x - (1)/(4))^2 = -(1)/(2) (x^2 - 2\((1)/(4)x + (1)/(16))`
  ==>
  `-(1)/(2) x^2 + (1)/(4)x - (1)/(32)`
  
• -1/2 ( x - 1/4 )² + 12 = 0
  ==>
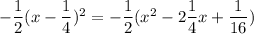
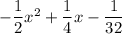
  `-(1)/(2) x^2 + (1)/(4)x - (1)/(32) + 12 = 0\\`
  
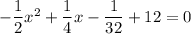
• Multiply both sides by 32
  ==> -16x² + 8x - 1 + 384 = 0
  ==> -16x² + 8x + 383 = 0 (Answer)
  with a = -16, b = 8 and c = 383