Question

ALGEBRA 1, SEMESTER 2

What is the average rate of change of the function over the interval x = 0 to x = 8?

f(x)=2x+33x−3
Enter your answer, as a fraction

Answer 1

So firstly, we have to find f(x) when x = 8 and x = 0. Plug the two numbers into the x variable of the function to solve for their f(x):

`f(0)=(2*0+3)/(3*0-3)\\ f(0)=(0+3)/(0-3)\\ f(0)=(3)/(-3)\\ f(0)=-1\\ \\ f(8)=(2*8+3)/(3*8-3)\\ f(8)=(16+3)/(24-3)\\ f(8)=(19)/(21)`

Now that we have their y's, we can use the slope, aka average rate of change, formula, which is
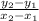`(y_2-y_1)/(x_2-x_1)` . Using what we have, we can solve it as such:

`((19)/(21)-(-1))/(8-0)=((40)/(21))/(8)=(40)/(21*8)=(40)/(168)=(5)/(21)`

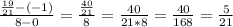
In short, the average rate of change from x = 0 to x = 8 is 5/21.