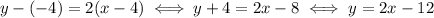Question

Write an equation in slope intercept form thag passes through (4,-4) and is parallel to 3+4x=2y-9

Answer 1

Let's deal with the slope first: we know that our line is parallel to the given line, and two lines are parallel if and only if their slopes are the same.

So, if we find the slope of the given line, we also have the slope of our line.

When a line is written in the form
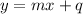`y=mx+q`, the slope is the coefficient
`m`.

So, we can rearrange the expression of the given line as follows:

`3+4x=2y-9 \iff 4x+12 = 2y \iff y = 2x+6`

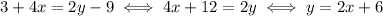
and so the slope is 2.

Now, when you know the slope
`m` and a point
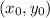`(x_0,y_0)` belonging to a line, you can write the equation of the line as

`y-y_0 = m(x-x_0)`

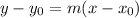
if you substitute your values, you have

`y-(-4) = 2(x-4) \iff y+4 = 2x-8 \iff y = 2x-12`

Answer 2

The original line is

4x - 2y = -12

The parallel lines will all be

4x - 2y = constant

and the constant is given by the point directly:

4x - 2y = 4(4) - 2(-4) = 24

2y = 4x - 24

y = 2x - 12

Answer: y = 2x - 12