Question

PLEASE HELP QUICK

Wires are attached to a pole to make it more secure. The diagram shows one of those wires having a length of 220 feet. The angle of elevation from the ground to the top of the pole is 36o. What is the height of the pole?

Answer 1

So if we make this a right triangle with the height of the pole being a leg and the wire that is making the pole more secure as the hypotenuse, we can then solve directly for the height of the pole.

Since we know the angle of elevation, the hypotenuse, and we are trying to find the height, we can use the trigonometric function, sine:

`sin(theta)=(opp)/(hyp)`

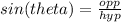
We must first convert 36 degrees into radians:

`Radians=(\pi)/(180)*degrees`

`Radians=(\pi)/(180)*36`

`Radians=0.62832`

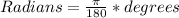
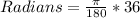
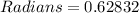
Then we can plug in the variables and solve for 'opp' or the height of the pole:

`sin(0.62832)=(opp)/(220)`

`220(sin(0.62832))=138.23`

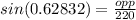
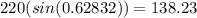
Therefore the height of the pole is 138.23 feet.

Answer 2

in(36)=h/220 ft

220 ft/in(36) = h

h=129.3 ft