Question

Prove a function that differs in finitely many points has the same integral as another

Answer 1

I'll show a proof if the two functions differ for only one point. Then, you can repeat the same argument in the neighbourhood of every other point.

So, suppose that we have

`f:[a,b]\to R,\quad g:[a,b]\to R,\quad \begin{cases} f(x) = g(x) &\text{ if } x\\eq x_0\\ f(x_0)\\eq g(x_0) \end{cases}`

We can write

`\displaystyle \int_a^b f(x)\; dx = \int_a^(x_0-\varepsilon) f(x)\; dx + \int_(x_0-\varepsilon)^(x_0+\varepsilon) f(x)\; dx + \int_(x_0-\varepsilon)^b f(x)\; dx`

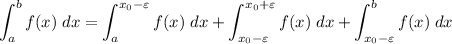
We can write the exact same thing for
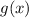`g(x)`, and we have (as far as we know)

`\displaystyle \int_a^(x_0-\varepsilon) f(x)\; dx = \int_a^(x_0-\varepsilon) g(x)\; dx,\ \int_(x_0-\varepsilon)^(x_0+\varepsilon) f(x) \\eq \int_(x_0-\varepsilon)^(x_0+\varepsilon) g(x)\; dx,\ \int_(x_0-\varepsilon)^b f(x)\; dx = \int_(x_0-\varepsilon)^b g(x)\; dx`

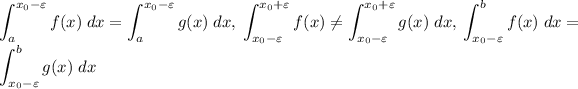
So, we only need to prove that the term where f and g are not the same function can be made arbitrarily small.

Since f and g are integrable on an interval, they are bounded. Let's call
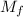`M_f` and
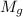`M_g` the maximum of f and g, respectively, in the interval
`[x_0-\varepsilon, x_0 + \varepsilon]`. We have

`\displaystyle \int_(x_0-\varepsilon)^(x_0 + \varepsilon) f(x)\; dx \leq \int_(x_0-\varepsilon)^(x_0 + \varepsilon) M_f\; dx = 2M_f\varepsilon`

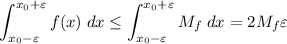
The same goes for g(x). So, You have

`\displaystyle \left|\int_a^b f(x)\;dx - \int_a^b g(x)\;dx\right| \leq 2(M_f+M_g)\varepsilon`

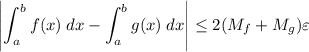
which tends to 0 as
`\varepsilon\to 0`