Answer:
we conclude that:
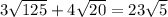
Hence, the last option i.e.
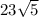 is correct.
is correct.
Explanation:
Given the expression
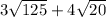
Combining the radical expressions
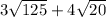
let us first solve
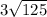
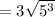
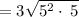
Apply radical rule:
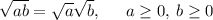
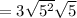
Apply radical rule:
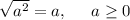
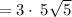
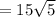
Thus,
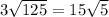
similarly solving
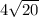
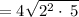
Apply radical rule:
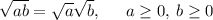
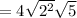
Apply radical rule:
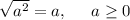
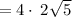
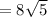
Thus,
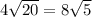
so we get
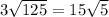
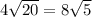
so the expression becomes
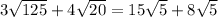 ∵
∵
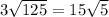 ,
,
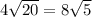
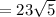 ∵
∵
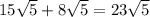
Therefore, we conclude that:
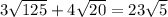
Hence, the last option i.e.
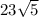 is correct.
is correct.