Question

Find the 66th term of the arithmetic sequence -10, 7, 24, ...

Answer 1

The answer is 1095.

66th term = 1095

Step-by-step explanation:

an = a1 + (n − 1)d

= -10 + (66 - 1) (17)

I did it on calculator.

It equals to = 1095

Answer 2

Answer: 1095

========================================

Step-by-step explanation:

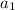`a_1` = -10 is the first term

d = 17 is the common difference. We add this amount to each term to get the next one. Eg: -10+17 = 7

We want to find the 66th term, so we'll use n = 66

Plug these values into the nth term arithmetic sequence formula below.

`a_n = a_1 + d(n-1)\\\\a_(66) = -10 + 17(66-1)\\\\a_(66) = 1095\\\\`

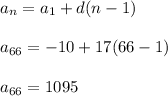
The 66th term is 1095