You can think of exponents as abbreviations for repeated multiplication. By that definition:
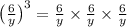
Which, by the properties of fraction multiplication, is the same thing as
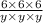
whiiiich, going back to our abbreviations, is the same thing as
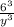
And since 6³ = 216, our final simplified answer is
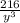
The most important discovery in this problem is the property that
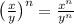
You could almost say that the exponent gets "distributed" to the numerator and denominator, and in fact, any exponents will have this property of "distributing" across multiplication or division.