Question

Which equation represents the relationship shown in the table?

Answer 1

Y=4x because 20/5 equals 4

Answer 2

The equation is y = 4x

Explanation:

From the table we can pick any 2 points
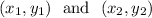`(x_1,y_1) \ \text{ and } \ (x_2, y_2)` such, we can obtain the slope of the line given 2 points using the following equation

`m  = \cfrac{y_2-y_1}{x_2-x_1}.`

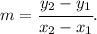
Then we can compare to the given options, or alternatively find the y-intercept using any point of the line, to get a line equation that looks like
`y = mx+b`

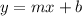
Finding the slope.

We can pick the first 2 points, that is (1,4) and (5, 20).

Replacing them on the slope equation give us,

`m=\cfrac{20-4}{5-1}`

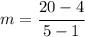
Simplifying we get

`m=\cfrac{16}{4}\\m=4`

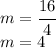
Thus the only option that has slope 4 is the line equation y = 4x which is the right answer for the exercise.