we are given
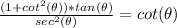
We will simplify left side and make it equal to right side
Left side:
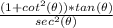
we can use trigonometric identity
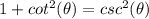
we can replace it
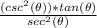
we know that
csc=1/sin and sec=1/cos
so, we can replace it
and we get
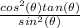
now, we know that
tan =sin/cos
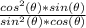
we can simplify it
and we get
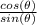
we can also write it as
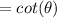
Right Side:

we can see that
left side = right side
so,
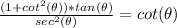 ......Answer
......Answer