1 Answer

Anish Agarwal · Answer 1 · 2019-02-18T04:36:55+0000

Formula for the volume of cone is
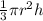
$(1)/(3) \pi r^2h$

Where r= radius of the cone

h = height of the cone

The value of pi is 3.14

Given volume of larger cone is 131 cm^3

Volume of larger cone =
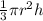
$(1)/(3) \pi r^2h$

131 =
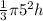
$(1)/(3) \pi 5^2h$

Solve for h

131 = 26.1667 *h

So h= 5 cm

The height of bigger cone = 5cm

Now we find the volume of smaller cone

Two cones similar so the sides are in proportional

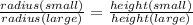
(radius(small))/(radius(large))= (height(small))/(height(large))

(2)/(5) =( height of small)/(5)

Height of smaller cone = 2cm

volume of smaller cone =
$(1)/(3) \pi 2^2*2$

= 8.38cm^3

Please log in or register to add a comment.