Question

What is the radius of the circle given the equation x 2 - 6x + y 2 + 10y - 2 = 0?

Answer 1

we are given

`x^2-6x+y^2+10y-2=0`

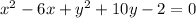
Firstly, we will change it into standard equation of circle

that is

`(x-h)^2 +(y-k)^2 =r^2`

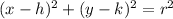
where r is radius

(h,k) is center

now, we can change our equation into this form

To change our equation into this form, we need to complete x square and y square

`x^2-6x+y^2+10y-2=0`

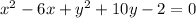
step-1: Move 2 on right side

`x^2-6x+y^2+10y-2+2=0+2`

`x^2-6x+y^2+10y=2`

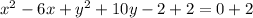
step-2: Complete x square

`x^2-2*3*x+y^2+10y=2`

`x^2-2*3*x+3^2+y^2+10y=2+3^2`

`(x-3)^2+y^2+10y=2+3^2`

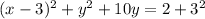
step-3: Complete y square

`(x-3)^2+y^2+2*5*y=2+3^2`

`(x-3)^2+y^2+2*5*y+5^2=2+3^2+5^2`

`(x-3)^2+(y+5)^2=2+3^2+5^2`

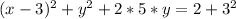
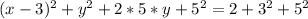
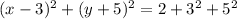
step-4: Combine right side terms

`(x-3)^2+(y+5)^2=36`

`(x-3)^2+(y+5)^2=6^2`

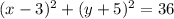
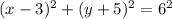
now, we can compare with our equation

and we will get

radius =r=6...............Answer

center=(h,k)=(3,-5)........................Answer