Question

What is 0.8333 forever in a fraction

Answer 1

`image`

Answer 2

There are a couple of different approaches you can use for this. Here's one.

1. Determine how many digits repeat. (There is just one repeating digit.)

2. Call your number x. Multiply x by 10 to the power of the number of digits found in step 1.

`x = 0.8\overline{3}\\10^(1)x=8.3\overline{3}`

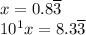
3. Subtract the original number, then solve for x.

`10x-x=9x=8.3\overline{3}-0.8\overline{3}=7.5\\\\x=(7.5)/(9)=(5)/(6)`

_____

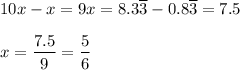
If you recognize that 0.333... (repeating) is 1/3, then you know that 0.0333... (repeating) is 1/10×1/3 = 1/30. Add that to 0.8 = 4/5 and you get

... 4/5 + 1/30 = 24/30 + 1/30 = 25/30 = 5/6