Question

If f(x)=(1/8)(8^x) what is f(3)?
A. 1/512
B. 1/64
C. 512
D. 64

Answer 1

Hi there!

Let's solve this problem step by step!

`f(x) = (1)/(8) (8 {}^(x))`

To find f(3) we must substitute x = 3 into the formula.

`f(3) = (1)/(8) (8 {}^(3) )`

Now we use PEMDAS (Parenthesis, exponents, multiply, divide, add, subtract) to find our answer.

Work out the exponents inside the parenthesis first.

`f(3) = (1)/(8) * 512`

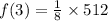
And finally multiply.

`f(3) = (1)/(8) * (512)/(1) = (512)/(8) = 64`

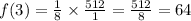
Hence, the answer is D. 64.
~ Hope this helps you!

Answer 2

D. 64

Explanation:

To evaluate the equation you just have to put the value given into the equation.

The equation given is:

f(x)=(
`(1)/(8)`)(
`8^(x)`)

So to evaluate f(3) you just put the 3 in the value of x

f(x)=(
`(1)/(8)`)(
`8^(3)`)

This would be equal to:

f(x)=(
`(1)/(8)`)(512)

Once you do the mutiplication you get:

f(x)=(
`(512)/(8)`)

And the answer would be:

f(x)=64