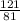Question

Geometric Series assistance

Answer 1

we have been asked to find the sum of the series

`\sum _(n=1)^5\left((1)/(3)\right)^(n-1)`

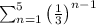
As we know that a geometric series has a constant ratio "r" and it is defined as

`r=(a_(n+1))/(a_n)=(\left((1)/(3)\right)^(\left(n+1\right)-1))/(\left((1)/(3)\right)^(n-1))=(1)/(3)`

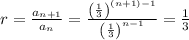
The first term of the series is
`a_1=\left((1)/(3)\right)^(1-1)=1`

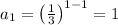
Geometric series sum formula is

`S_n=a_1(1-r^n)/(1-r)`

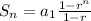
Plugin the values we get

`S_5=1\cdot (1-\left((1)/(3)\right)^5)/(1-(1)/(3))`

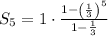
On simplification we get

`S_5=(121)/(81)`

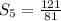
Hence the sum of the given series is
`(121)/(81)`