Question

Using the equation representing the height of the firework (h = -16t2 + v0t + h0), algebraically determine the extreme value of f(t) by completing the square and finding the vertex. Interpret what the value represents in this situation.

Answer 1

`h(t)=-16t^2+v_0t+h_0`

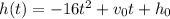
The idea is to write the equation of the parabola in vertex form, i.e. in the form that immediately tells you where the vertex of the parabola. The extreme value (minimum or maximum) of the parabola occurs at the
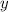`y`-coordinate of the vertex. Whether this point is a minimum or a maximum is determined by the sign of the leading coefficient; in this case, that coefficient is -16, which means the parabola is "opening" downward so that the vertex is the maximal point.

The general form would be

`h(t)=-16(t-a)^2+b`

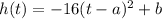
where the vertex is located at
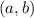`(a,b)`. There are two useful ways we can do this.

(1) We can work backwards and solve for
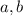`a,b` by expanding the expected vertex form.

`-16(t-a)^2+b=-16(t^2-2at+a^2)+b=-16t^2+32at-16a^2+b`

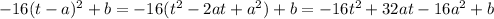
This tells us we need to have

`\begin{cases}32a=v_0\\b-16a^2=h_0\end{cases}\implies a=(v_0)/(32),b=h_0+\frac{{v_0}^2}{64}`

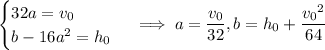
(2) We could also work forwards, starting with the given equation for
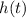`h(t)` and completing the square:

`-16t^2+v_0t+h_0=-16\left(t^2-(v_0)/(16)t-(h_0)/(16)\right)`

`=-16\left(t^2-(v_0)/(16)t+\frac{{v_0}^2}{32^2}-\frac{{v_0}^2}{32^2}-(h_0)/(16)\right)`

`=-16\left(\left(t-(v_0)/(32)\right)^2-\frac{{v_0}^2}{32^2}-(h_0)/(16)\right)`

`=-16\left(t-\underbrace{(v_0)/(32)}_a\right)^2+\underbrace{\frac{{v_0}^2}{64}+h_0}_b`

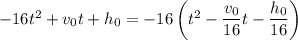
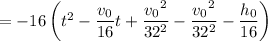
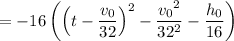
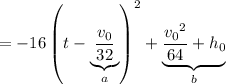
which is the same expression we ended up with before. Using either method, we find that the vertex is
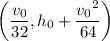`\left((v_0)/(32),h_0+\frac{{v_0}^2}{64}\right)`, giving an extreme value of
`h_0+\frac{{v_0}^2}{64}`.

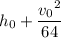The expression
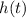`h(t)` tells you the height
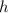`h` of the firework at a specific time
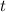`t`. From the vertex form we've derived above, we've shown that the greatest height that the firework can achieve is determined exactly by its launch velocity
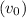`(v_0)` and how high the firework was when it was launched
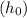`(h_0)`.